Potrzebę modelowania wielowymiarowego najlepiej uświadamia następujący problem. Powiedzmy, że kierowcy z dużych miast powodują więcej wypadków niż kierowcy z wiosek. Wiadomo też, że ludzie o wyższych zarobkach mają więcej wypadków niż ludzie o niższych zarobkach. Być może należy więc wprowadzić zniżkę dla mieszkańców wsi i dla ludzi o niższych zarobkach. Tak się jednak składa, że mieszkańcy wsi to ci sami ludzie, których sklasyfikowaliśmy jako osoby o niskich zarobkach. Przy wprowadzaniu zmian w taryfie należy więc uważać, by tej samej grupy nie obdarować obiema zniżkami. Problem komplikuje się dodatkowo, gdy korelacje pomiędzy cechami dotyczą trzech, czterech lub dwudziestu zmiennych.
Modelowanie wielowymiarowe GLM
W naszej pracy z takimi problemami spotykamy się wielokrotnie. Narzędziem stosowanym przez nas najczęściej w tego typu analizach są GLM, czyli Uogólnione Modele Regresji Liniowej (ang. Generalized Linear Models). Metoda ta jest standardowym sposobem wyceny stosowanym w krajach UE i w USA i coraz bardziej popularnym w Polsce. Podejście to jest promowane przez amerykańskie Casualty Actuarial Society.
Sytuację z przykładu przedstawia poniższy wykres uzyskany w systemie Pretium/SAS. Pomarańczowa linia pokazuje zalecane zniżki i zwyżki wynikające z modelu jednowymiarowego. Widzimy, że model ten znacznie zaniża koszt ubezpieczenia dla dużych mieszkań. Właściwą – wielowymiarową – wartość zwyżki pokazuje linia zielona.
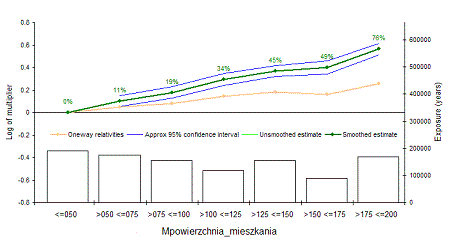
Jeden z naszych modeli: zależność wysokości szkód kradzieżowych od powierzchni mieszkania, model jednowymiarowy (linia pomarańczowa) i wielowymiarowy (linia zielona). Wykres z programu Pretium.
Innym problemem, z którym spotykają się ubezpieczyciele, mogą być skomplikowane interakcje pomiędzy zmiennymi. Na przykład poniższy wykres przedstawia typową sytuację w ubezpieczeniach samochodowych zamodelowaną w systemie Emblem. Widzimy tu złożoną, częściową interakcję pomiędzy szkodowością, płcią i wiekiem kierowcy. Widać, że mężczyźni powodują więcej szkód komunikacyjnych niż kobiety, ale tylko dopóki są młodzi.
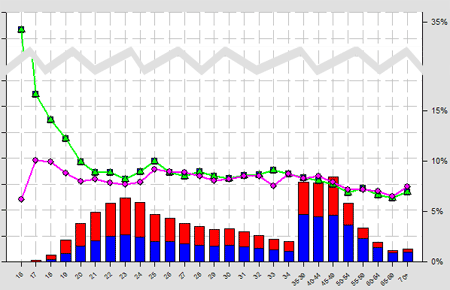
Częściowa interakcja w modelu płci i wieku w ubezpieczeniach samochodowych. Szkodowość mężczyzn (linia zielona) istotnie różni się od szkodowości kobiet (linia fioletowa) tylko dopóki nie osiągną oni wieku ok. 27 lat. Standardowy przykład z programu Emblem.
Ubezpieczyciele, którzy potrafią dobrze zrozumieć takie i podobne zjawiska na rynku, mogą kształtować swoja politykę cenową tak, by przyciągnąć do siebie lepsze ryzyka. Gorsze ryzyka można albo zostawić dla konkurencji, albo nadal je ubezpieczać, ale po odpowiedniej cenie.
Inne metody modelowania
W naszych projektach najczęściej stosujemy także inne metody modelowania takie jak:
- metody oparte na teorii wiarygodności (ang. credibility), jako jedyne lub jako pomocnicze podejście w zależności od sytuacji klienta,
- metody oparte na analizie geograficznej / terytorialnej,
- modelowanie franszyzy w oparciu o czynnik redukcyjny (ang. loss elimination ratio).